→Minimization: adding levenberg-marquardt wikipedia link |
including the video |
||
| Line 1: | Line 1: | ||
=Dynamic PSF= | |||
Dynamic PSF is a dynamic tool inspired by the PixInsight routine of the same name. It is used to fit unsaturated stars whithin the image. For now, the PSF model is restricted to a 2D Gaussian function which is sufficient in most cases. | Dynamic PSF is a dynamic tool inspired by the PixInsight routine of the same name. It is used to fit unsaturated stars whithin the image. For now, the PSF model is restricted to a 2D Gaussian function which is sufficient in most cases. | ||
<html5media width="750">http://free-astro.vinvin.tf/videos/DPSF.webm</html5media> | |||
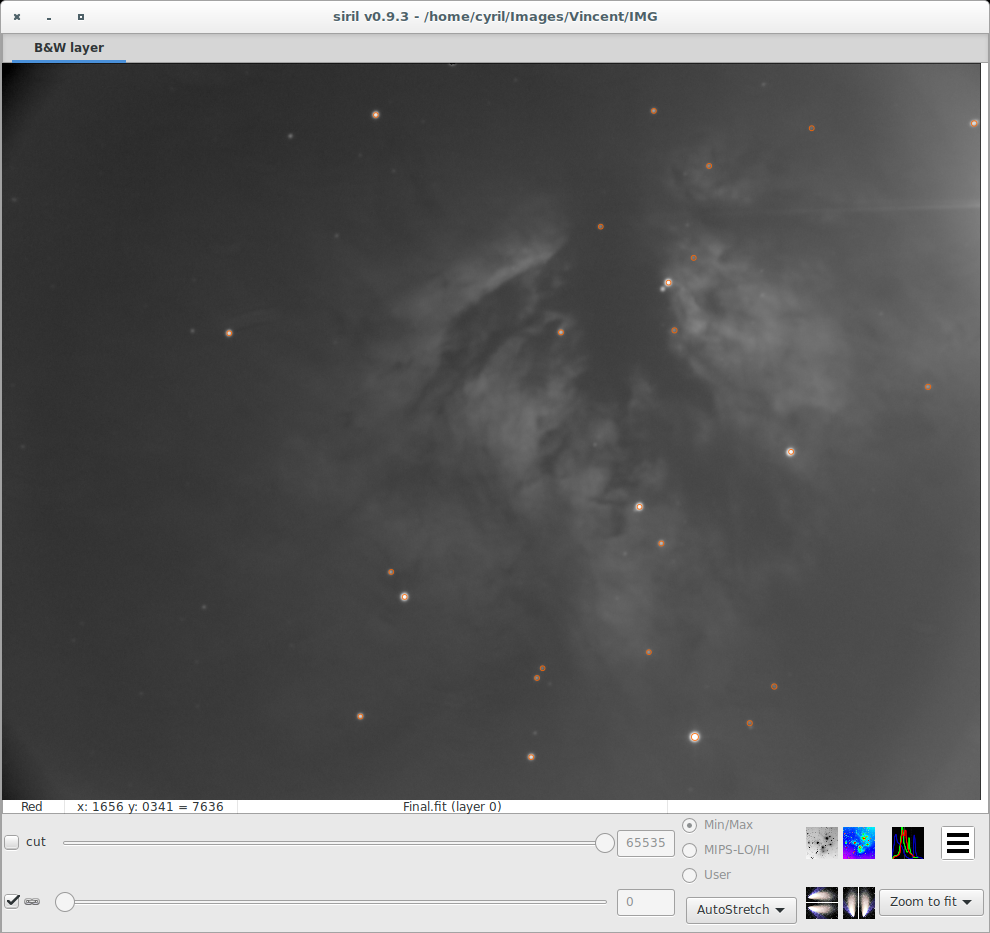
Example star detection in an image (50% scale, the stars are closely surrounded by orange circles): | |||
[[File:Siril_BW.png]] | [[File:Siril_BW.png]] | ||
Revision as of 02:36, 23 February 2014
Dynamic PSF
Dynamic PSF is a dynamic tool inspired by the PixInsight routine of the same name. It is used to fit unsaturated stars whithin the image. For now, the PSF model is restricted to a 2D Gaussian function which is sufficient in most cases.
<html5media width="750">http://free-astro.vinvin.tf/videos/DPSF.webm</html5media>
Example star detection in an image (50% scale, the stars are closely surrounded by orange circles):
Model
- 2D Gaussian:
[math]\displaystyle{ G(x,y)=B+A e^{-\left( \frac{(x-x_0)^2}{2\sigma^2_x} + \frac{(y-y_0)^2}{2\sigma^2_y} \right)} }[/math]
- Parameters:
- [math]\displaystyle{ B }[/math]: The average local background in the [0, 1] range.
- [math]\displaystyle{ A }[/math]: The maximal intensity of the star in the [0, 1] range: this is the peak value of the fitted function, located at the centroid coordinates x0 and y0.
- [math]\displaystyle{ x_0 }[/math] and [math]\displaystyle{ y_0 }[/math]: The centroid coordinates in pixel units, which is the position of the center of symmetry of the fitted PSF.
- [math]\displaystyle{ \text{FWHM}_X }[/math] and [math]\displaystyle{ \text{FWHM}_Y }[/math]: The Full Width Half Maximum on the X and Y axis in pixel units. These parameters are calculated as follow :
- [math]\displaystyle{ \text{FWHM}_X = 2\sigma_x\sqrt{2\log{2}} }[/math]
- [math]\displaystyle{ \text{FWHM}_Y = 2\sigma_y\sqrt{2\log{2}} }[/math]
- It is possible to obtain the FWHM parameters in arcseconds units. This requires you fill all fields corresponding to your camera and lens/telescope focal in the setting parameter window. If standard FITS keywords FOCALLEN, XPIXSZ, YPIXSZ, XBINNING and YBINNING are read in the FITS HDU, the PSF will also compute the image scale in arcseconds per pixel.
- [math]\displaystyle{ r }[/math]: The roundness parameter. It is expressed as [math]\displaystyle{ \text{FWHM}_Y/\text{FWHM}_X }[/math], with [math]\displaystyle{ \text{FWHM}_X\gt \text{FWHM}_Y }[/math] the symmetry condition.
- Angle: The rotation angle of the X axis with respect to the centroid coordinates in the [-90, 90] range. The angle [math]\displaystyle{ \theta }[/math] is computed as follow:
- [math]\displaystyle{ x' = +x cos \theta + y sin \theta }[/math]
- [math]\displaystyle{ y' = -x sin \theta + y cos \theta }[/math]
- RMSE: This is an estimation of fitting quality. The smaller the RMSE is, the better the function is fitted.
Minimization
Minimization is performed with a non-linear Levenberg-Marquardt algorithm thanks to the very robust GNU Scientific Library[1]. As a first step, the algorithm runs a set of parameters excluding rotation angle in order to set good start values and thus, avoiding possible divergence. If [math]\displaystyle{ \sigma_x-\sigma_y \gt 0.01 }[/math] (parameters directly computed in the 2-D Gaussian formula, see above), then another fit is run with the angle parameter. Therefore, the Siril Dynamic PSF provides accurate values for all the fitted parameters.
Use
Dynamic PSF can be called from two different ways depending on what you want:
- You may want to fit just one star. In this case, after drawing a selection around an unsaturated star (this is important for the accuracy of the result) you can either type "PSF" in the prompt of the console or do a right click and choose the "PSF" item. In both case you will be able to copy the result and paste it where you want. In this cased a relative magnitude is computed following [math]\displaystyle{ -2.5\times \log I }[/math] where [math]\displaystyle{ I }[/math] is the total intensity of the fitted star.
- In the case you want to deal with many stars and average it, you MUST work on the dynamic PSF window by ever clicking on the "Analysis" menu and the "Dynamic PSF" item or drawing a selection around an unsaturated star, doing a right click and selecting the "Pick a star" item.
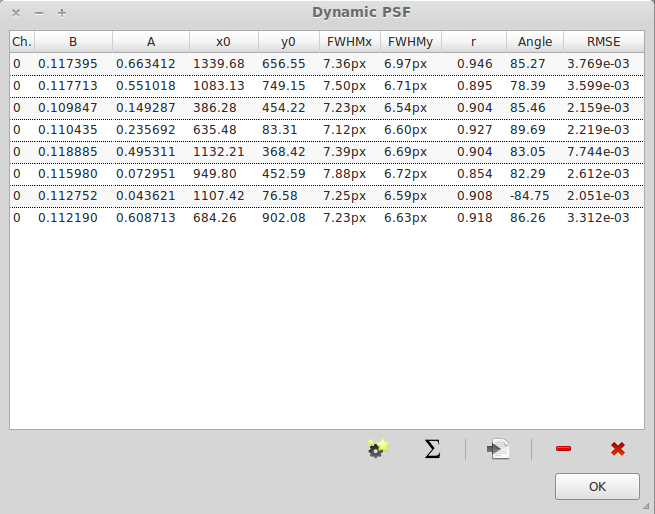
The dynamic PSF window is shown and provides very valuable tools:
- You can select and/or remove a star chosing it in a tree list.
- You can export the result of the PSF in ASCII file.
- You can run the star detection algorithm by clicking on the corresponding button.
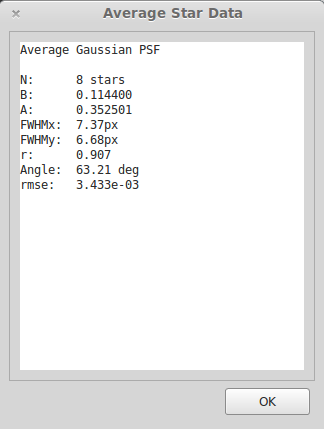
- You can average the PSF results and copy and paste the result.
Star detection
As said before, this dynamic PSF also contains an automatic tool of star detection. This algorithm is based on the publication of Mighell, J. J.[2] which is a simple peak detector algorithm indentifying any pixel that is greater than any of its eight neighbors. In addition to this basic algorithm, a PSF is applied on every possible "detected stars" and Siril rejects all detected structures that don't fulfill a set of prescribed detection criteria. Finaly, a circle is drawn around detected stars. Nevertheless, if a non-stellar object is selected, it is possible to select it and remove it from the list. You may notice that during the automatic star detection, no rotation angle are fitted due to speed consideration.
References
- ↑ http://www.csse.uwa.edu.au/programming/gsl-1.0/gsl-ref_35.html
- ↑ Mighell, K. J. 1999, in ASP Conf. Ser., Vol. 172, Astronomical Data Analysis Software and Systems VIII, eds. D. M. Mehringer, R. L. Plante, & D. A. Roberts (San Francisco: ASP), 317.